Sisu

• Kiirjuhend
• Sammud
• Näpunäited
• Hoiatused

Kahe maatriksi korrutamise teadmine on teel pooleks, kuidas õppida maatriksit teisega jagama. Sõna "jaga" kirjutatakse jutumärkidesse, kuna maatriksit ei saa tehniliselt jagada. Selle asemel peate maatriksi korrutama tagurpidi teine. Kui see tundub kummaline, siis mõelge sellele ideele levinumate matemaatiliste mõistete osas: 10 ÷ 5 arvutamise asemel on võimalik võtta 5 (5 või /₅), arvutage 10 x 5 ja saate sama vastuse. Sel põhjusel peetakse selle matemaatika haru jagamiseks kõige lähemal maatriksiks korrutamist maatriksi pöördväärtusega. Neid arvutusi kasutatakse tavaliselt lineaarvõrrandite süsteemide lahendamiseks.

Kiirjuhend

1. Maatriksijaotust pole määratletud. Selle asemel korrutage esimene maatriks teisega. Kirjutage probleem ÷ ümber kui * või *.
2. Kui maatriks ei ole ruudukujuline või kui selle determinant on võrdne nulliga, kirjutage "pole ühte lahendit". Muidu leidke determinant ja jätkake järgmise sammuga.
3. Arvutage väärtus (pöördvõrdeline).
4. * Või * arvutamiseks korrutage maatriksid. Tea, et see ei pruugi tingimata anda sama vastust.

Sammud

1. osa 3-st: jagamise võimalikkuse kinnitamine

1. 

   
   
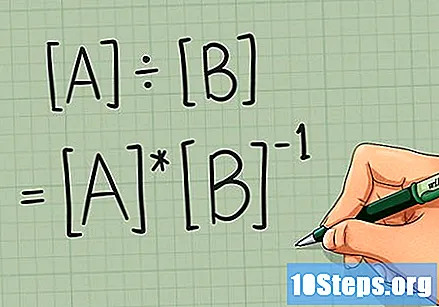
   Mõista maatriksi "jagunemist". Tehniliselt sellist kontseptsiooni ei eksisteeri. Maatriksi jagamine teisega on määratlemata funktsioon. Lähim vaste on korrutamine teise maatriksi pöördvõrrandiga. Teisisõnu, kuigi ÷ pole määratletud, on võimalik arvutada *. Kuna need kaks võrrandit oleksid skalaarses suuruses ekvivalentsed, näib see välja nagu maatriksijaotus, kuid oluline on kasutada õiget terminoloogiat.
   • Pange tähele, et * ja * pole üks ja sama probleem. Võimalike lahenduste leidmiseks peate võib-olla mõlemad arvutama
   • Näiteks kirjuta selle asemel, et kirjutada.
     Võimalik, et peate arvutama ka vastuse, mille vastus võib olla erinev.

2. 

   
   
   Veenduge, et jagamismaatriks on ruudukujuline. Maatriksi pöördväärtuse saamiseks peab see olema ruudukujuline, sama arvu ridade ja veergudega. Vastasel juhul pole probleemile ühte lahendust.
   • Mõiste "jagamismaatriks" on natuke ebamäärane, kuna tehniliselt ei ole see jagamise probleem. * Puhul tähendab see maatriksit. Kasutatud näites on see maatriks.
   • Maatriksit, millel on pöördvõrrand, nimetatakse "ümberpööratavaks" või "mitte-ainsuseks". Massiivid, millel pole pöördvõrde, on "ainsused".

3. 

   
   
   Kontrollige, kas kahte maatriksit saab korrutada. Selleks peab esimese maatriksi veergude arv olema võrdne teises maatriksis olevate ridade arvuga. Kui see kummaski seadistuses ( * või *) ei toimi, pole probleemil lahendust.
   • Näiteks kui see on 4 x 3 maatriks ja see on 2 x 2 maatriks, siis pole lahendust. * ei saa arvutada, kuna 4 ≠ 2 ja * ei saa ka, kuna 2 ≠ 3.
   • Pange tähele, et käände käändes on alati sama arv ridu ja veerge kui algses maatriksis. Selle sammu lõpuleviimiseks pole vaja pöördväärtust arvutada.
   • Kasutatud näites on mõlemad maatriksid 2 x 2, nii et neid saab korrutada suvalises järjekorras.

4. 

   Leidke 2 x 2 maatriksi determinant. Enne maatriksi pöördpildi võtmist on veel üks nõue kontrollida. Selle determinant ei saa olla null. Vastasel juhul pole maatriksil pöördvõrdelist. Siit saate teada, kuidas kõige lihtsamal juhul, 2 x 2 maatriks, leida determinant:
   • 2 x 2 maatriks: määraja on ad-bc. Teisisõnu, võtke toode peamisest diagonaalist (vasakult ülaservalt paremale), seejärel lahutage toode pöörddiagonaalist (ülevalt paremalt vasakule alumisse serva).
   • Näiteks maatriksil on determinant (7) (3) - (4) (2) = 21 - 8 = 13. See ei ole arv null, seega on võimalik leida vastupidine.

5. 

   Leidke suurema maatriksi determinant. Kui maatriks on 3 x 3 või suurem, võtab determinandi leidmine pisut rohkem tööd:
   • Maatriks 3 x 3: valige suvaline element ja kriipsutage läbi rida ja veerud, kuhu see kuulub. Leidke järelejäänud 2 x 2 maatriksi determinant, korrutage see valitud elemendiga ja märgi määramiseks viige maatriksgraafi tähisele. Korrake seda toimingut kahel järgmisel elemendil samas reas või veerus nagu esimene valitud element, seejärel lisage kolm määrajat. Lugege seda artiklit ja lugege samm-sammult ning näpunäiteid selle protsessi kiirendamiseks.
   • Suuremad massiivid: soovitatav on kasutada graafikukalkulaatorit või tarkvara. Meetod sarnaneb 3 x 3 maatriksiga, kuid käsitsi valmistamine võtab kauem aega. Näiteks 4 x 4 maatriksi determinandi leidmiseks peate leidma nelja 3 x 3 maatriksi determinandid.

6. 

   Jätkub. Kui maatriks ei ole ruudukujuline või kui selle determinant on võrdne nulliga, kirjutage "pole ühte lahendit". Probleem on täielik. Kui maatriks on ruudukujuline ja selle determinant ei ole null, liikuge järgmisele jaole järgmise sammu leidmiseks: otsige vastupidist.

Osa 2/3: maatriksi ümberpööramine

1. 

   Muutke peamiste diagonaalelementide positsioone 2 x 2. Kui maatriks on 2 x 2, saate selle arvutamise hõlpsamaks muutmiseks kasutada otsetee. Selle otsetee esimene samm hõlmab vasakus ülanurgas oleva elemendi asendamist paremas alanurgas oleva elemendiga. Näiteks: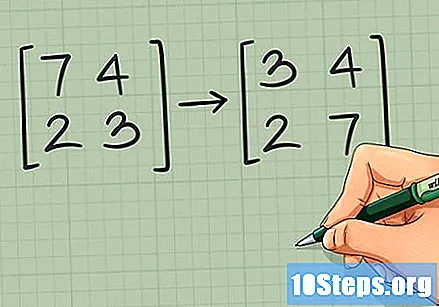
   • →
   • Märge: Enamik inimesi kasutab 3 x 3 või suurema maatriksi pöördväärtuse leidmiseks kalkulaatorit. Kui soovite arvutamist käsitsi teha, vaadake jaotise lõppu.

2. 

   Võtke ülejäänud kahe elemendi vastand, kuid jätke need oma kohale. Teisisõnu, korrutage ülemises "paremas" ja alumises "vasakus" nurgas olevad elemendid -1: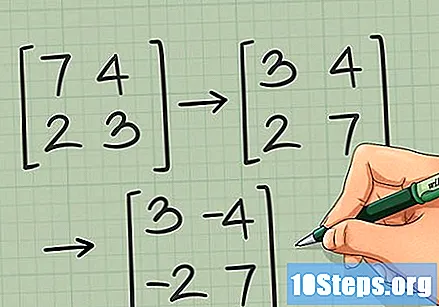
   • →

3. 

   Võtke determinandi vastastikune väärtus. Selle maatriksi determinandi leidsite ülaltoodud jaotises, nii et pole vaja seda uuesti teha. Kirjutage lihtsalt vastastikune 1 / (determinant):
   • Näites on determinant 13. Selle vastastikune väärtus on.

4. 

   Korrutage uus maatriks determinandi vastastikusega. Korrutage uue maatriksi iga element äsja arvutatud vastastikusega. Saadud maatriks on 2 x 2 maatriksi pöördväärtus:
   • 
     =

5. 

   Kontrollige, kas inversioon on õige. Selleks korrutage pöördväärtus algmaatriksiga. Kui vastupidine väärtus on õige, on produkt alati maatriksiga identne. Kui kõik on korras, jätkake probleemi lõpetamiseks järgmise jaotisega.
   • Kasutatava näite korral korrutage.
   • Vaadake artiklit Kuidas maatriksit korrutada, kui vajate abi.
   • Märkus: maatriksi korrutamine ei ole kommutatiivne, see tähendab, et tulemust mõjutab tegurite järjekord. Maatriksi korrutamisel selle pöördvõrrandiga saadakse mõlemal variandil identiteedimaatriks.

6. 

   Vaata selles artiklis kuidas ümber pöörata 3 x 3 või suuremat maatriksit. Kui te pole seda protsessi esimest korda õppinud, säästke aega, kasutades graafikute kalkulaatorit või matemaatikatarkvara, et teha matemaatikat suuremate maatriksitega. Kui te ei pea arvutamist käsitsi tegema, on siin ühe meetodi lühijuhend:
   • Pange identiteet I maatriks teie maatriksist paremale. Näiteks →. Identifitseerimismaatriksil on element "1" koos peamise diagonaaliga ja "0" elemendiga ilma kõigi muude positsioonideta.
   • Maatriksi redigeerimiseks toimige ridade kaupa, kuni vasak külg on astmeliselt vormis, seejärel jätkake redigeerimist, kuni vasak külg on identne identsusmaatriksiga.
   • Operatsiooni lõpus on maatriks kuju. Teisisõnu, parem külg pööratakse algsest maatriksist ümber.

Osa 3/3: Maatriksite korrutamine probleemi lahendamiseks

1. 

   Kirjutage kaks võimalikku võrrandit. Skaalaarsete suurustega "tavalises matemaatikas" on korrutamine kommutatiivne; 2 x 6 = 6 x 2. Sama ei kehti maatriksite kohta, nii et peate arvutama kaks probleemi:
   • * on lahendus x probleemi jaoks x = .
   • * on lahendus x probleemi jaoks x = .
   • Kui see on osa võrrandist, siis tehke mõlemal küljel sama toiming. Kui =, siis ei on võrdne, kuna see asub vasakul, aga paremal.

2. 

   Leidke vastuse mõõtmed. Lõpliku maatriksi mõõtmed on kahe teguri välismõõtmed. Sellel on sama arv ridu kui esimesel maatriksil ja sama arv veerge kui teisel maatriksil.
   • Tulles tagasi algse probleemi juurde, mis puutub 2 x 2 maatriksisse, siis on vastuse mõõtmed ka 2 x 2.
   • Keerukama näite kasutamiseks, kui see on massiiv 4 x 3 ja on 3 x maatriks 3, siis * maatriksil on 4 x 3 mõõtmeid.

3. 

   Arvutage esimese elemendi väärtus. Täpsemad juhised leiate ülaltoodud artiklist või värskendage oma mälu järgmise kokkuvõttega:
   • 1. rea ja 1. veeru leidmiseks leidke 1. rea ja 2. veeru punktide korrutis. See tähendab, et arvutage 2 x 2 maatriksi korral.
   • Kasutatud näites on vastuse 1. rea 1. veerg järgmine:
     
     
     

4. 

   Korda skalaarprodukti maatriksi igas positsioonis. Näiteks positsioonis 2.1 olev element on rea 2 ja veeru punkti punktkorrutus. Proovige näide ise lõpule viia. Peaksite saama järgmised vastused:
   • Kui teil on vaja leida mõni muu lahendus,

Näpunäited

• Maatriksi saab jagada skalaarhulgaga, jagades maatriksi iga elemendi kogusega.
  • Näiteks maatriks jagatud 2 =

Hoiatused

• Kalkulaatorid ei ole maatriksi arvutamisel alati 100% täpsed. Näiteks kui kalkulaator teatab, et element on väga väike arv (näiteks 2E), on väärtus tõenäoliselt null.